The Settler's Dilemma - Betrayed again by a 4 in Catan

Does this situation sound familiar? You decide to play a “casual” game of Settlers of Catan with some friends and begin to set up the board. Throughout the setup process, you study the map and carefully place your initial settlements, maximizing your resource allocation and the probabilities associated with each hex. Looking at the board and your opponents’ placements, you feel great. Maybe you’ve even grabbed some 6s and 8s for ore and wheat, along with some expansion opportunities to nearby ports. Victory feels inevitable.

Then the actual game starts and everything unravels. One of your prized initial placements, an 8 hex that should be supplying you with a steady stream of ore, never seems to hit, while 4s roll ceaselessly. Before you know it, the game is over and you’ve lost. If you’re playing online and are anything like me, you scrutinize the post-game report that Colonist.io, an online host for Catan, provides, directing your friends to the screen displaying the dice roll distribution to prove that 4s really were rolled more times than 8s (of course you never complain without cause). Why does it feel like this happens so often, and what can we do about it? Below, I’ll provide a quick overview of Catan, a data-driven analysis of dice distributions, and some tips for managing randomness in the game going forward.

Settlers of Catan Overview

For the uninitiated, Settlers of Catan is a board game where players compete to build settlements, cities, and roads by collecting and trading five types of resources. The board is modular and driven by dice rolls, which dictate the resource production each turn. At the start of each game, the hexes are randomly arranged on the board and bear a picture that illustrates the type of resource they generate. All of the hexes are also labeled with the numbers 2 through 12, indicating the dice rolls that triggers their production. Players race each other to reach 10 victory points by expanding their territory, acquiring development cards (similar to chance cards), and strategically trading or blocking opponents.

If you haven’t experienced Catan yet and this sounds at all interesting to you, I encourage you to try it out.

Example Catan Map

Opening strategy

The outcome of the game is heavily influenced by your starting position, and as the board configuration changes in each game, the players take time studying the map and strategically placing their initial settlements one after another.

I asked ChatGPT for its perspective on the optimal placement strategy and thought it gave a tactically sound response:

1. Resource coverage: hit as many of the five resources as you can with your two settlements.
2. Production probability: stack high-pip numbers (6 / 8 / 5 / 9) for a combined pip count of 16–18+.
3. Number diversity: spread your numbers so you’re not hostage to one roll.
4. Expansion potential: leave yourself roads to ports or missing resources.
5. Strategy alignment: if you lack brick + wood, lean into dev-card play (wheat + ore + sheep).
6. Opponent disruption: deny key intersections or cut routes—without wrecking your own game.

From my perspective, numbers 1, 2, and 5 from the above are generally the most important ingredients to a game-winning strategy. Most of the people that I have played with tend to first look at the high probability hexes, and then examine the resource distribution as a supporting consideration. A lack of resource diversity can easily tank your game even if you hold all of the 6s and 8s on the board.

Gameplay - where the dice break down

Now that we’ve aligned on the opening strategy, let’s dive into dice distributions.

As in most board games, Catan relies on a pair of six-sided dice to determine resource generation. Remembering our high school/college/graduate school stats class, there are 36 outcomes in this situation and the distribution should look like the below. For example, there are 5 different ways for the dice to sum to 6, leading to a probability of 5/36 or 13.9%.

Theoretical distribution

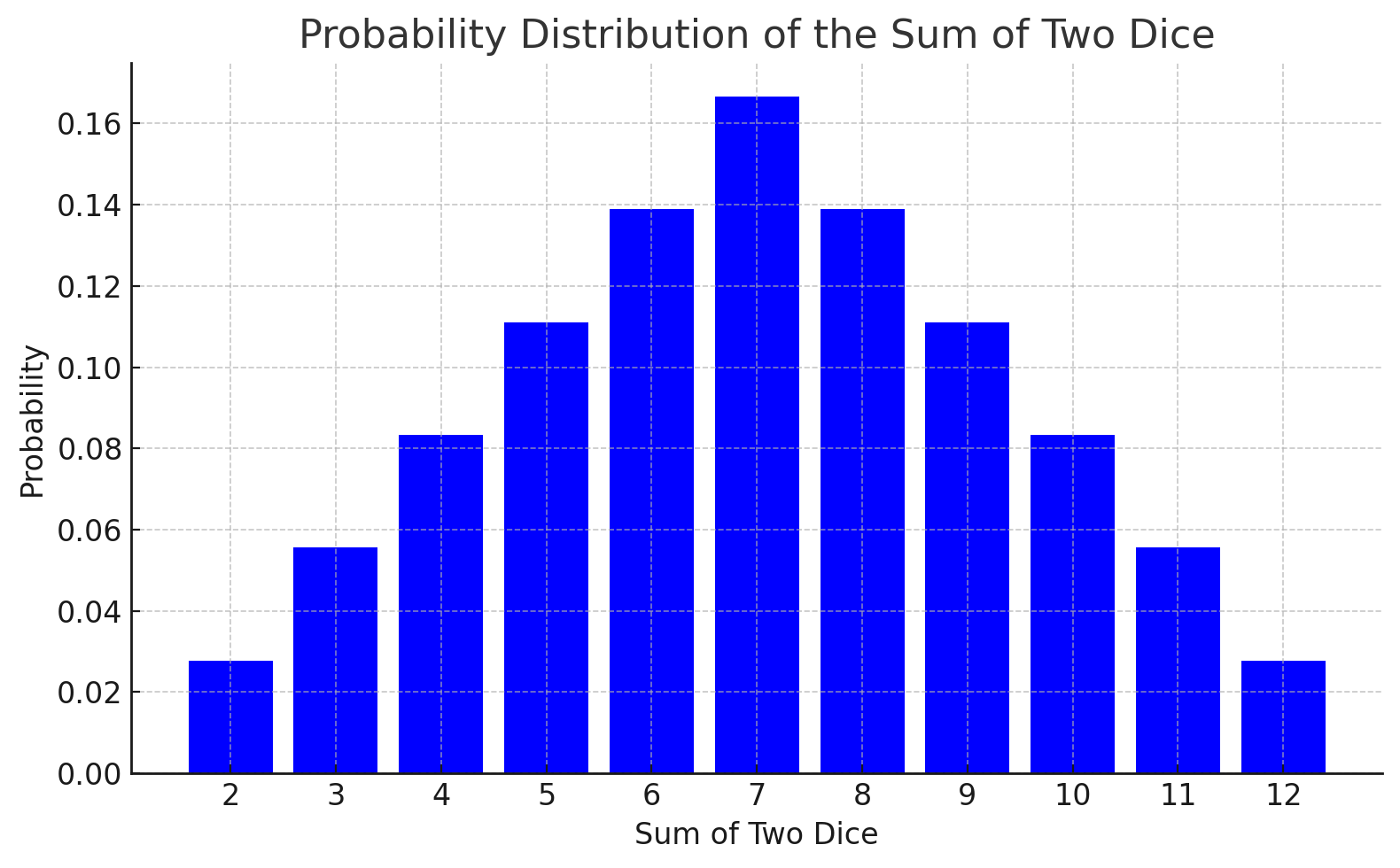
This theoretical distribution is symmetrical with a peak in the middle. Given that there are no hex tiles with 7s in Catan, the 6s and 8s should generally be the most desirable spaces. Although this graph should look familiar to most students of probability, it may be unrecognizable or naïve to frequent Catan players

Based on the number of players, a typical game of Catan can last anywhere from 50-80 turns on average. To illustrate how the dice distribution can play out in practice, I ran 4 simulations with 50 rolls each and plotted the outcomes. For easy comparison, I overlayed the theoretical distribution with a black line on each graph.

Distributions for 50 rolls

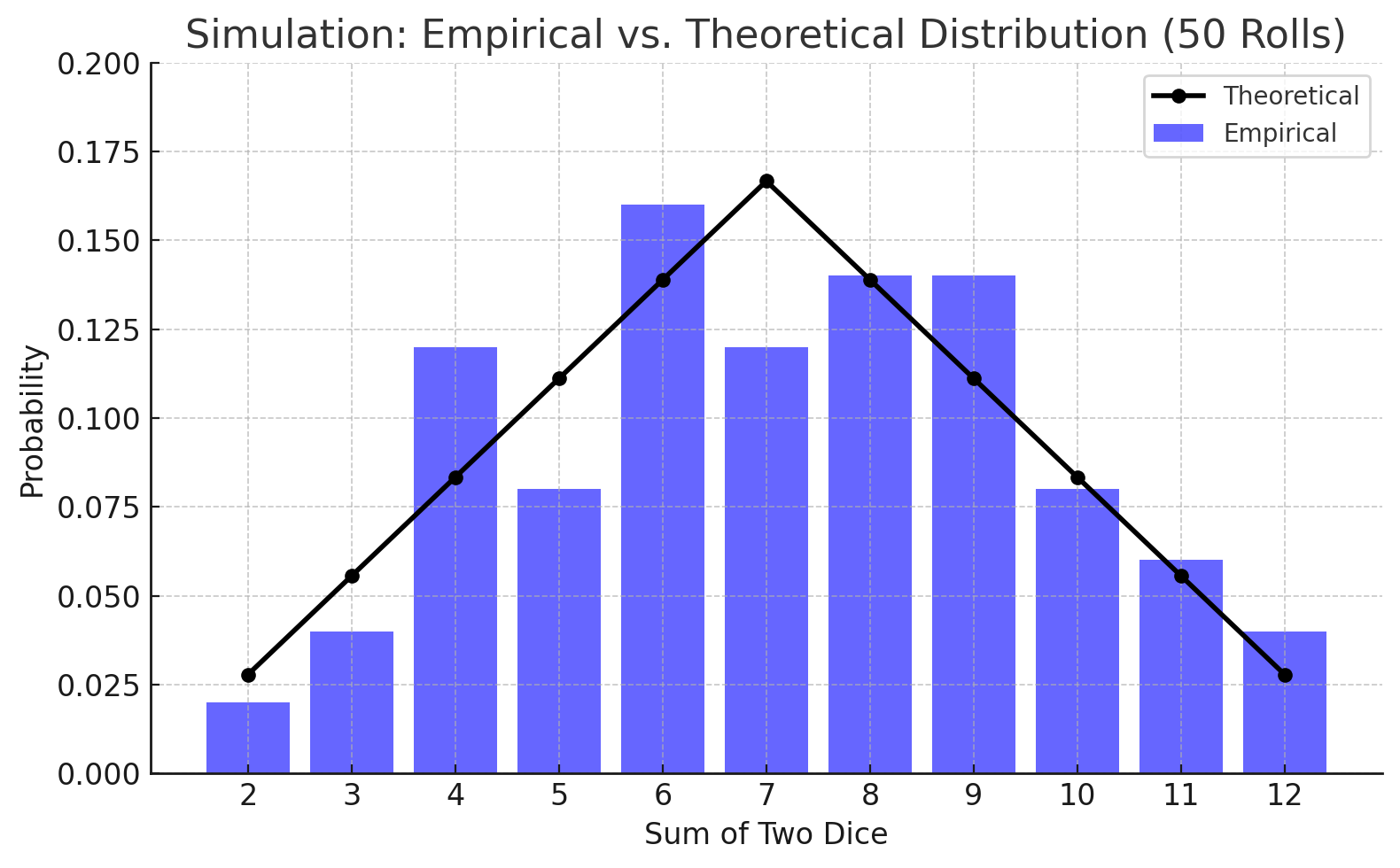
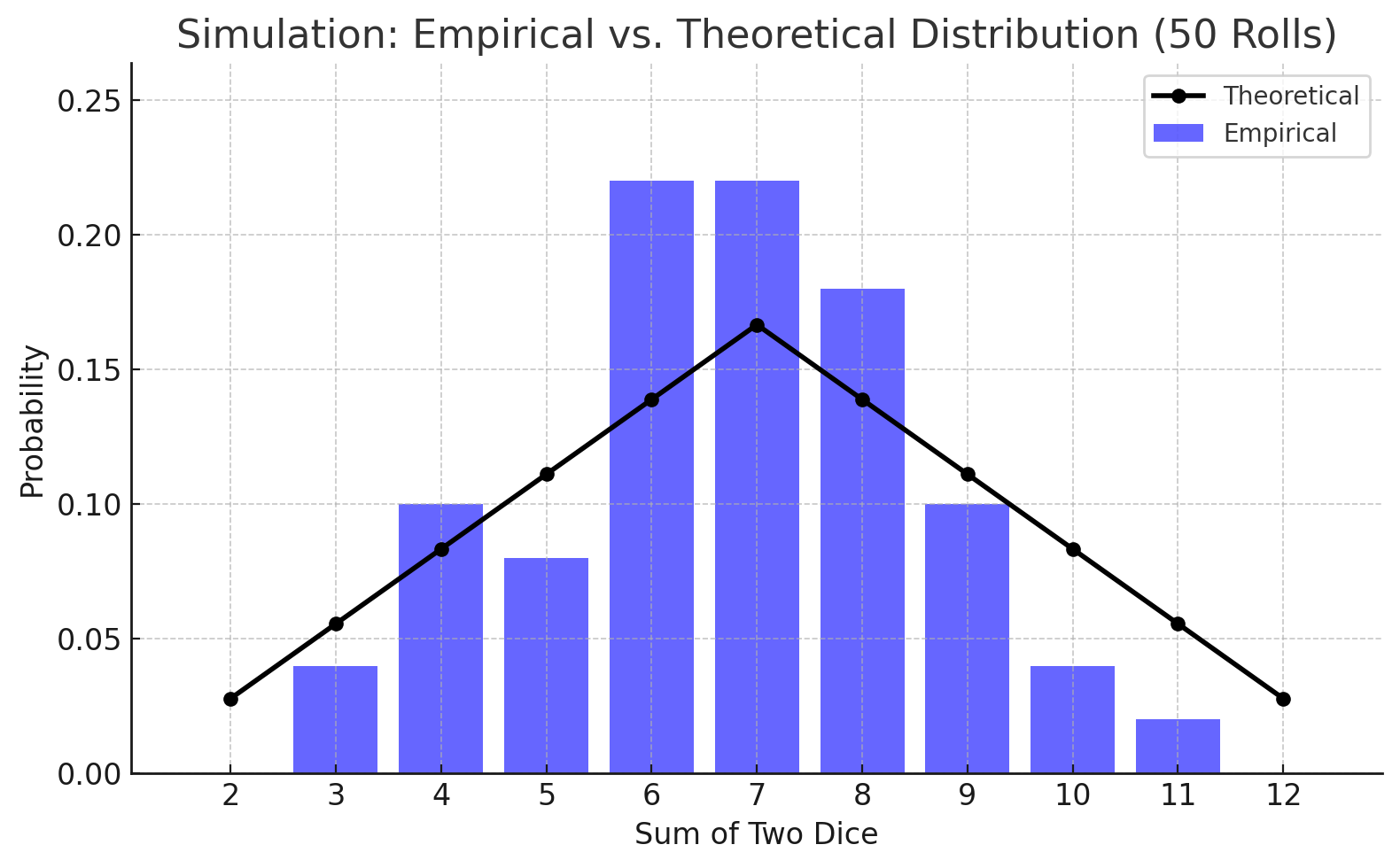
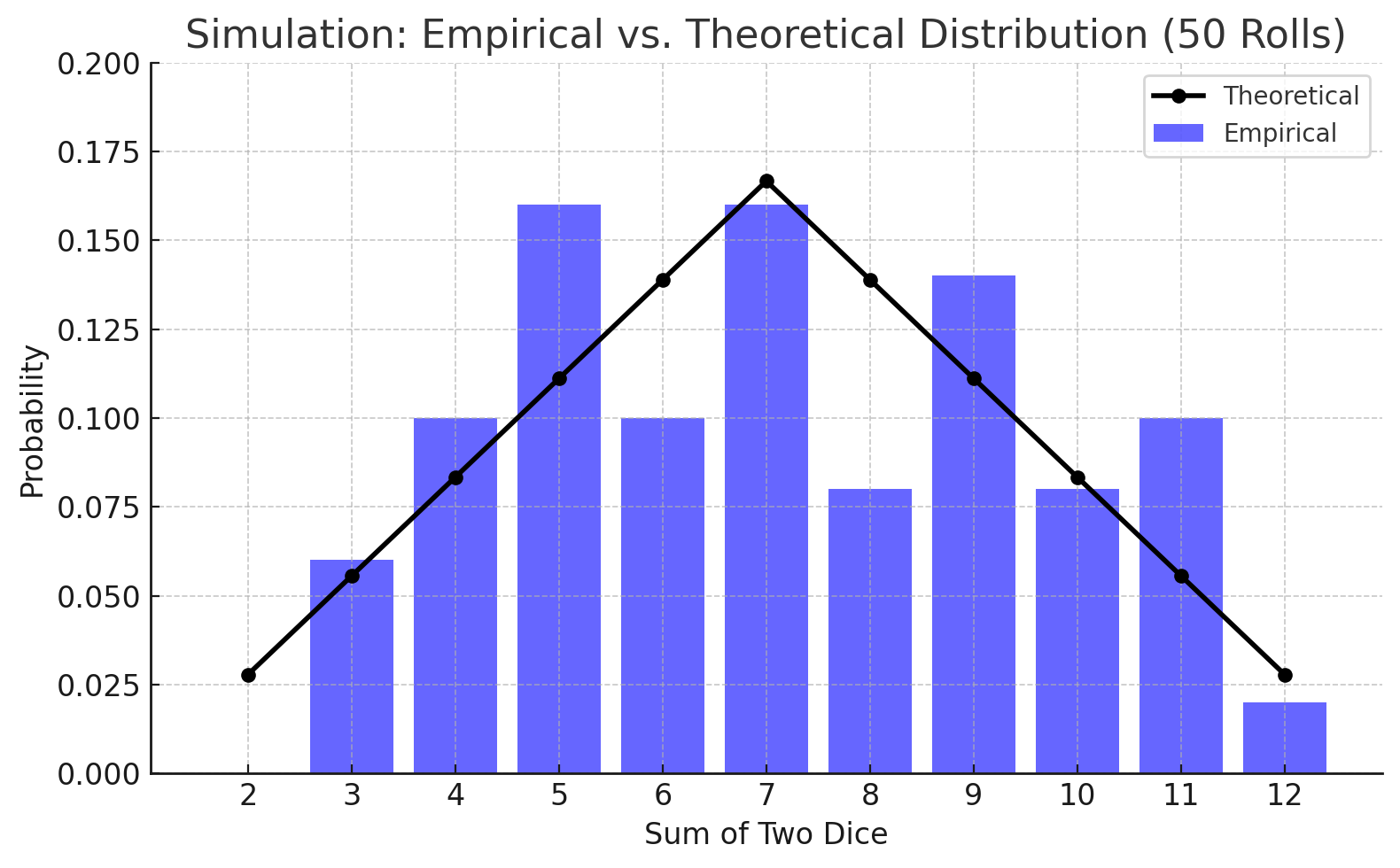
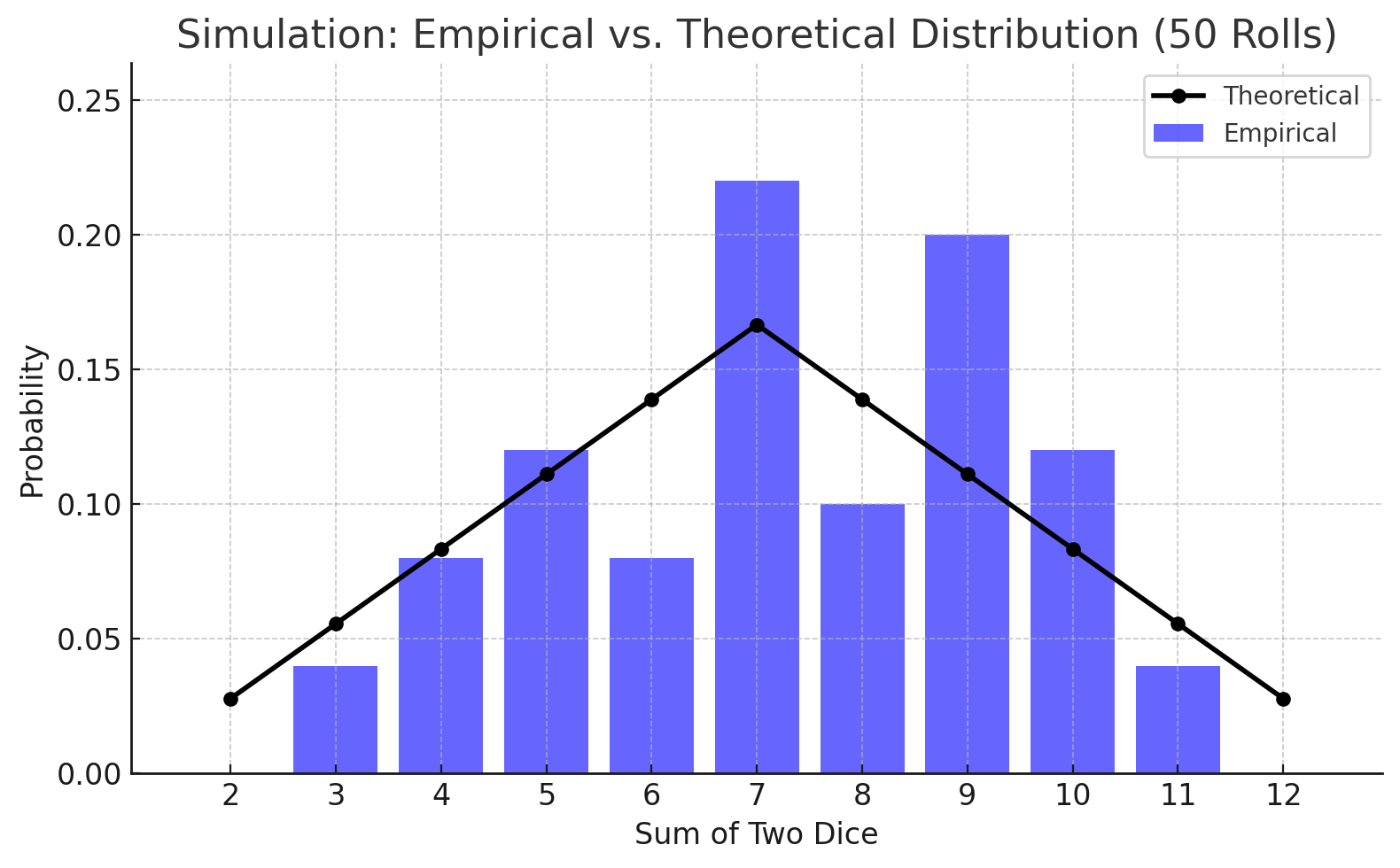
The above distributions can be considered the set of dice rolls for 4 simulated games with 50 turns each. The top two distributions vary somewhat from the theoretical version, but I don’t think they would elicit a huge reaction from game participants (e.g., in the top right distribution, the low probability 2s and 12s are never even rolled).

Let’s spend a bit more time looking at the bottom two distributions. The bottom left chart is a prime example of the type of dice distribution that could exasperate even the most stoic of Catan players. Immediately we can notice that the distribution differs from the neatly symmetrical theoretical shape. In this simulated game, 4s, 5s, 9s, and 11s were rolled as often or more than 6s and 8s. Generally hexes with 11s are avoided at all costs, but the lucky player who parked a piece there earned more resources than those on the 6 and 8 hexes. The bottom right distribution shows a similar funkiness, as the 9s and 10s are rolled more frequently than 6s and 8s.

Now, let’s steadily increase the number of rolls for each simulation. Given the law of large numbers, we expect the distributions to converge towards theoretical values as the number of rolls grows.

Distributions for 100 rolls

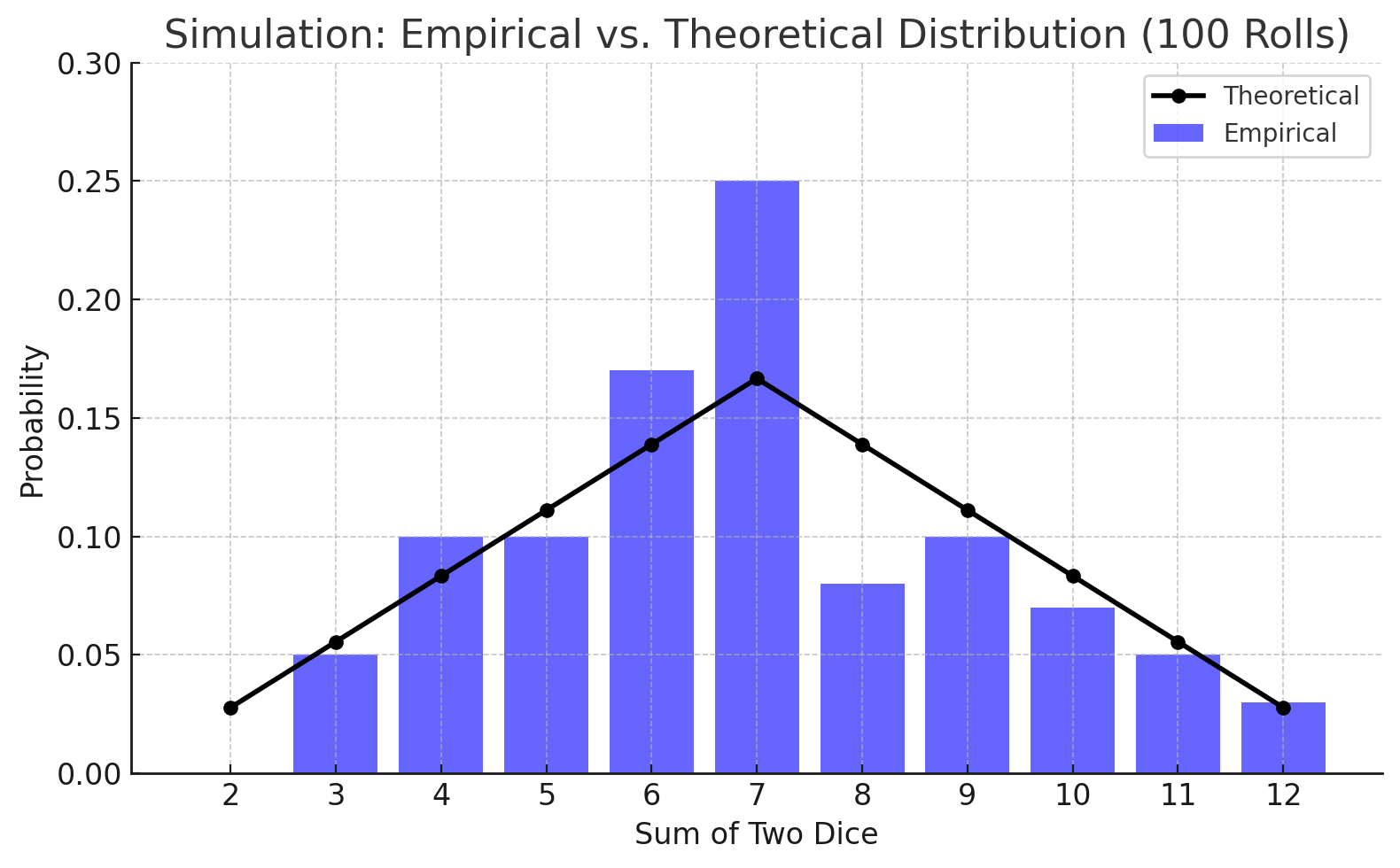
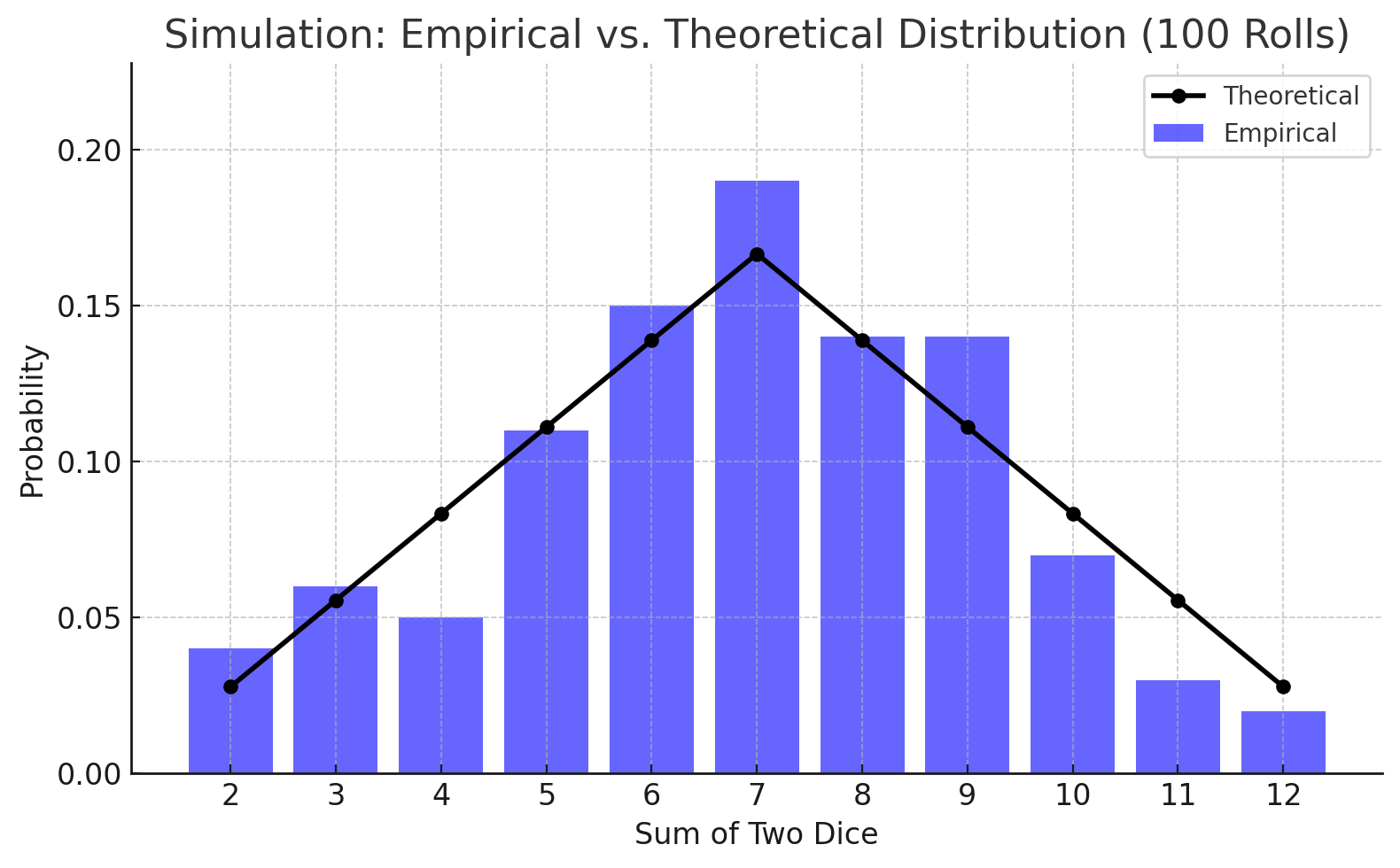
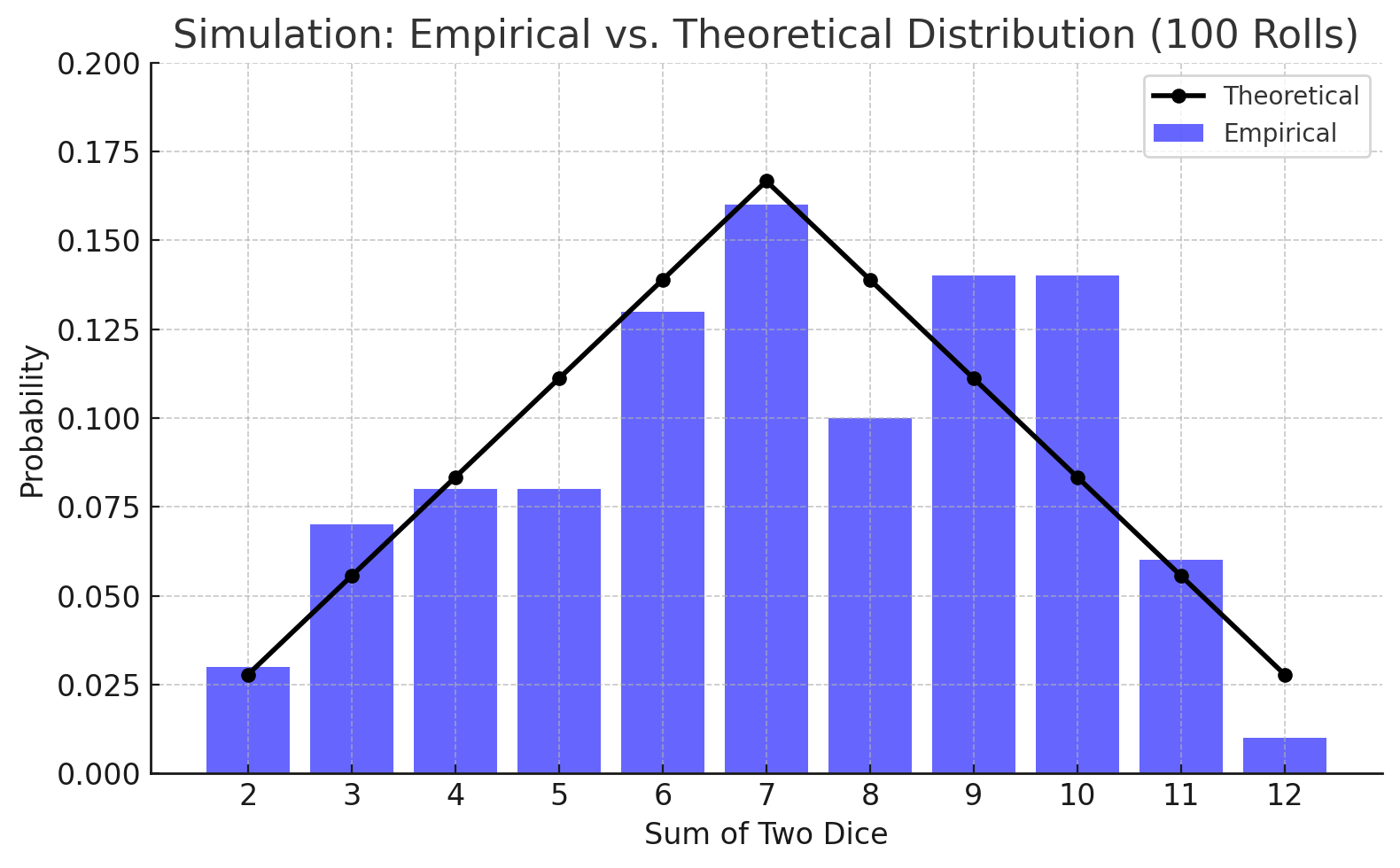
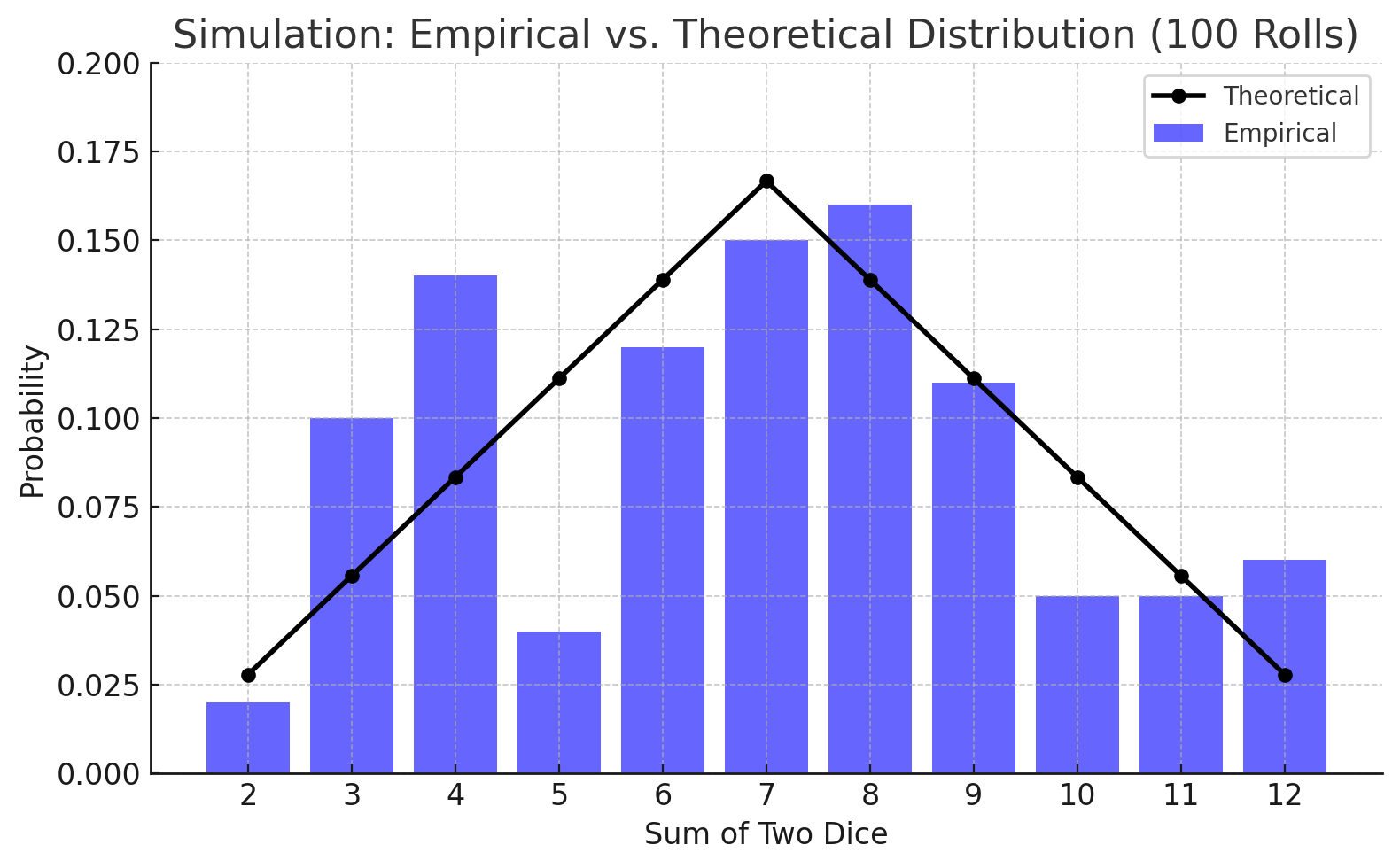
Even after doubling the number of rolls, we still see distributions that differ from the theoretical values. For example, in the bottom right chart, the number of 3s and 4s rolled keeps pacing with values that should have higher theoretical probability.

Let’s continue increasing the number of rolls in each simulation…

Distributions for 200 rolls

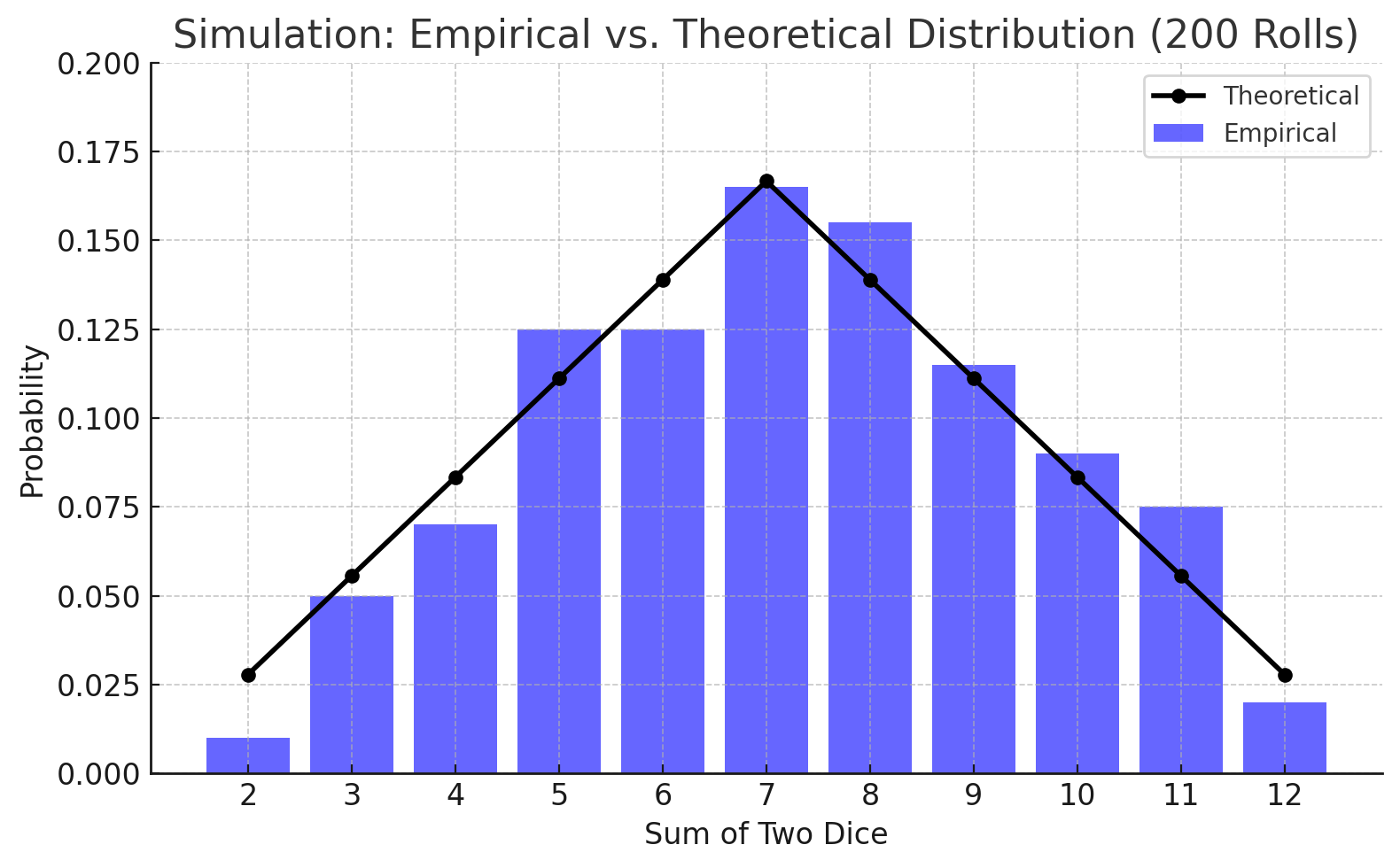
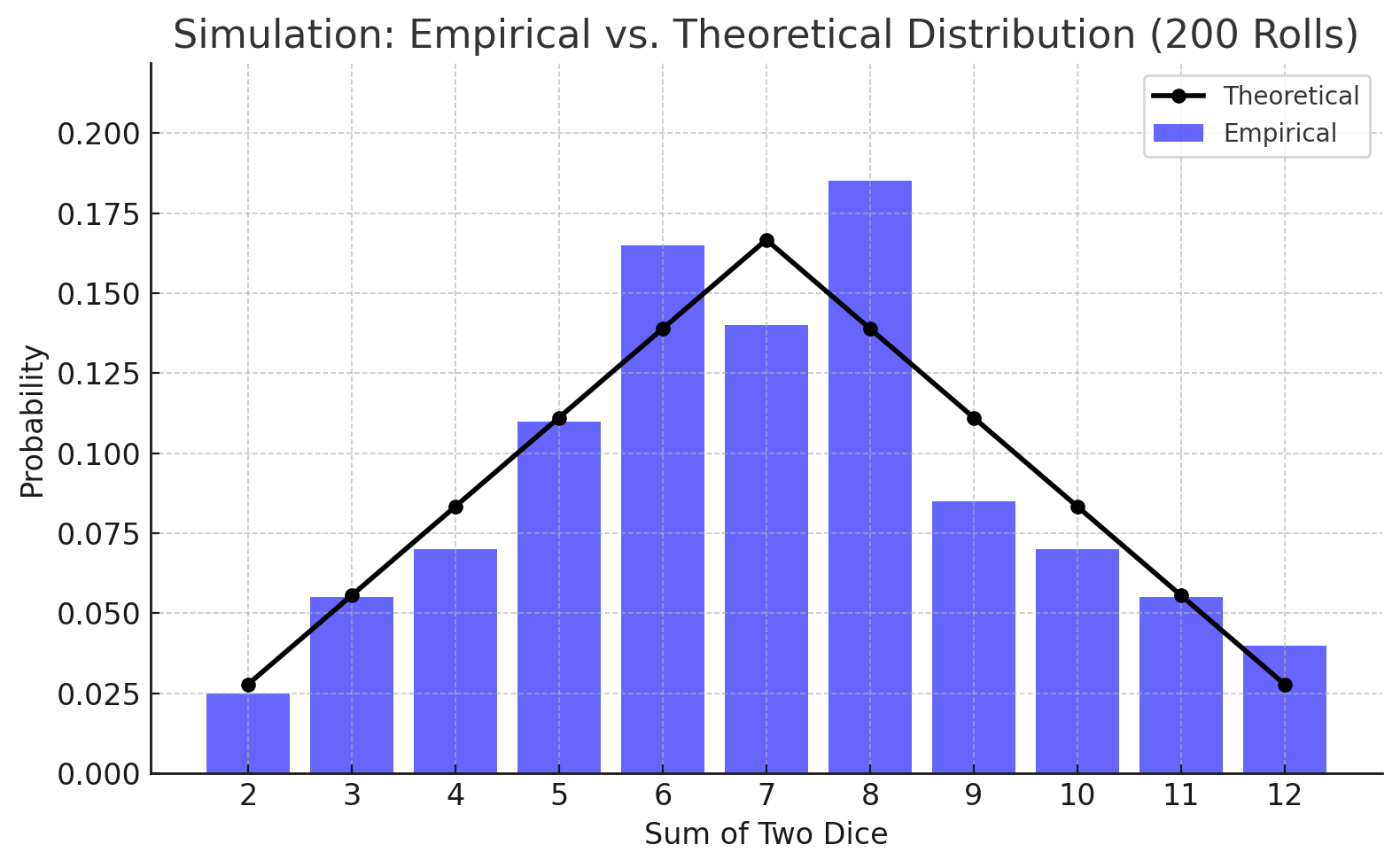
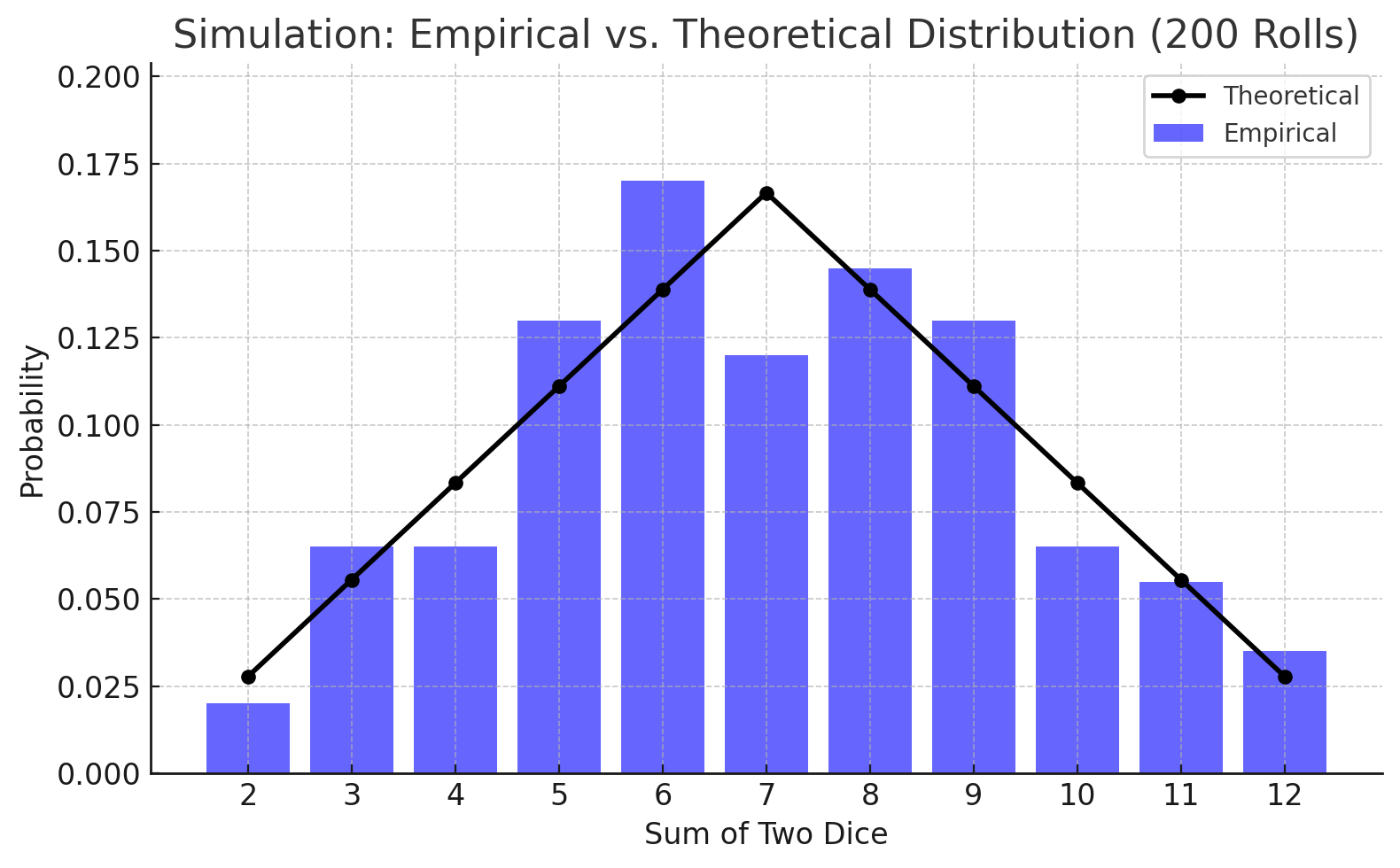
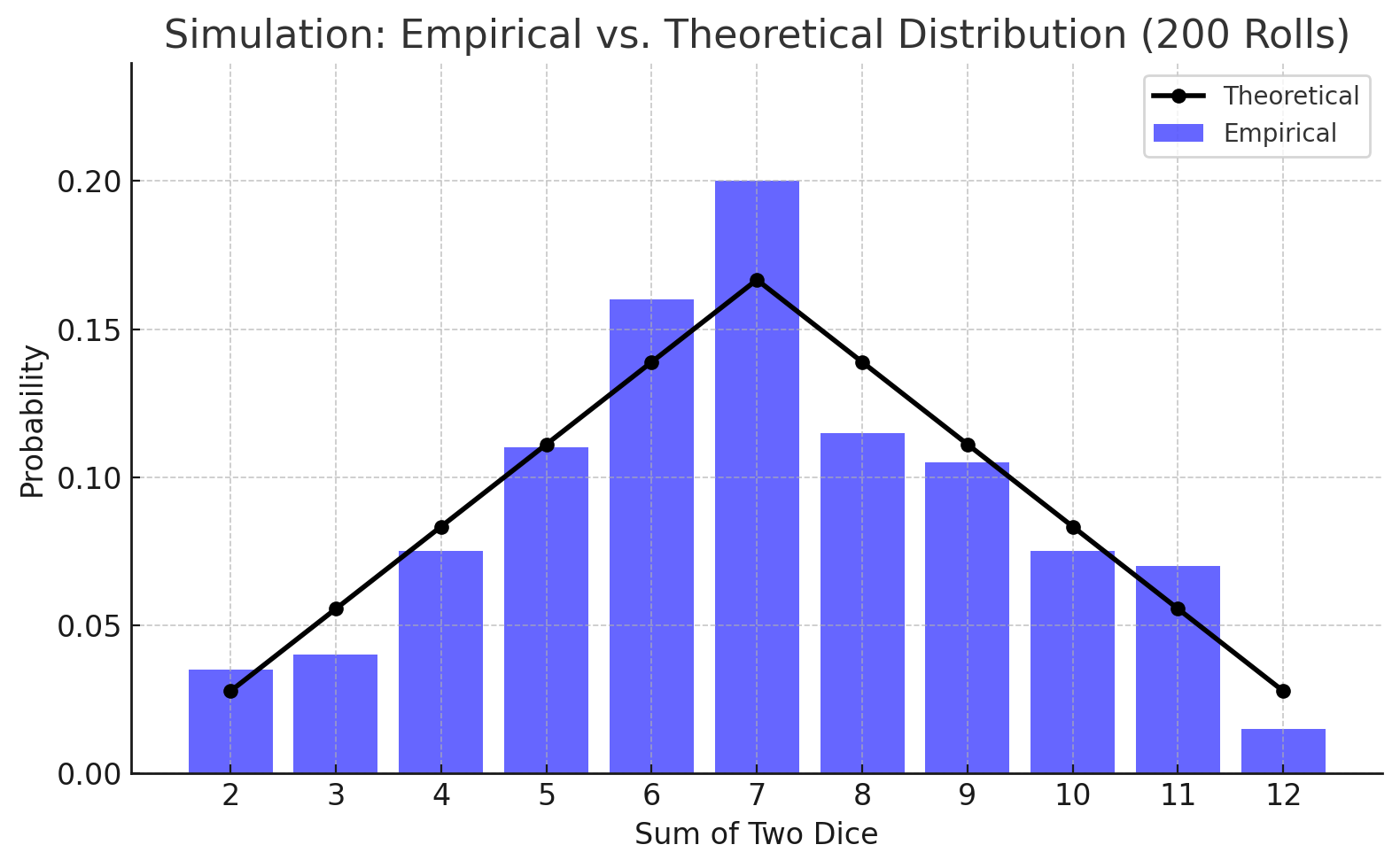
After 200 rolls, it has become more difficult to quickly point to charts where the empirical distribution markedly differs from the theoretical distribution.

Just for fun, let’s keep growing the roll count…

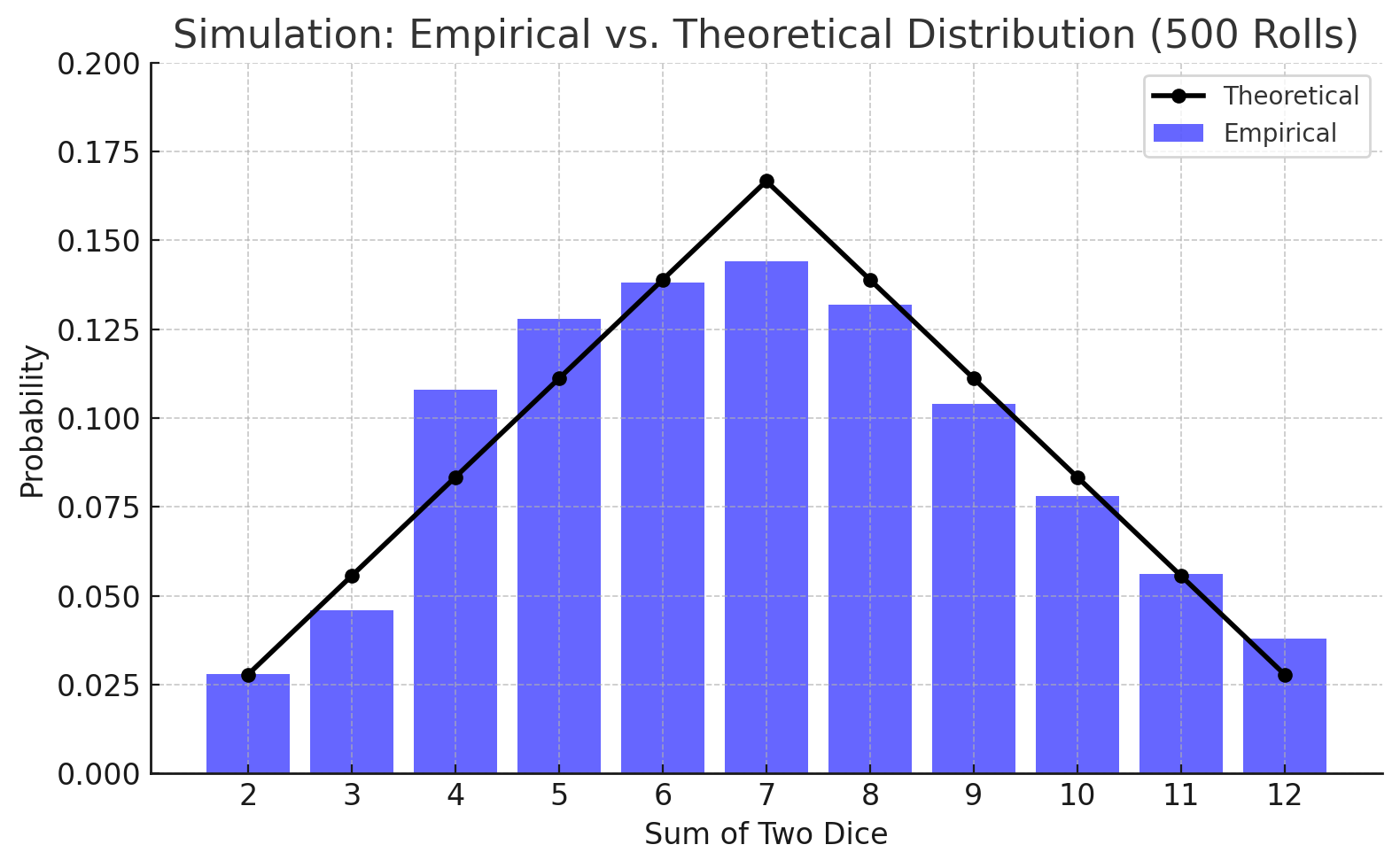
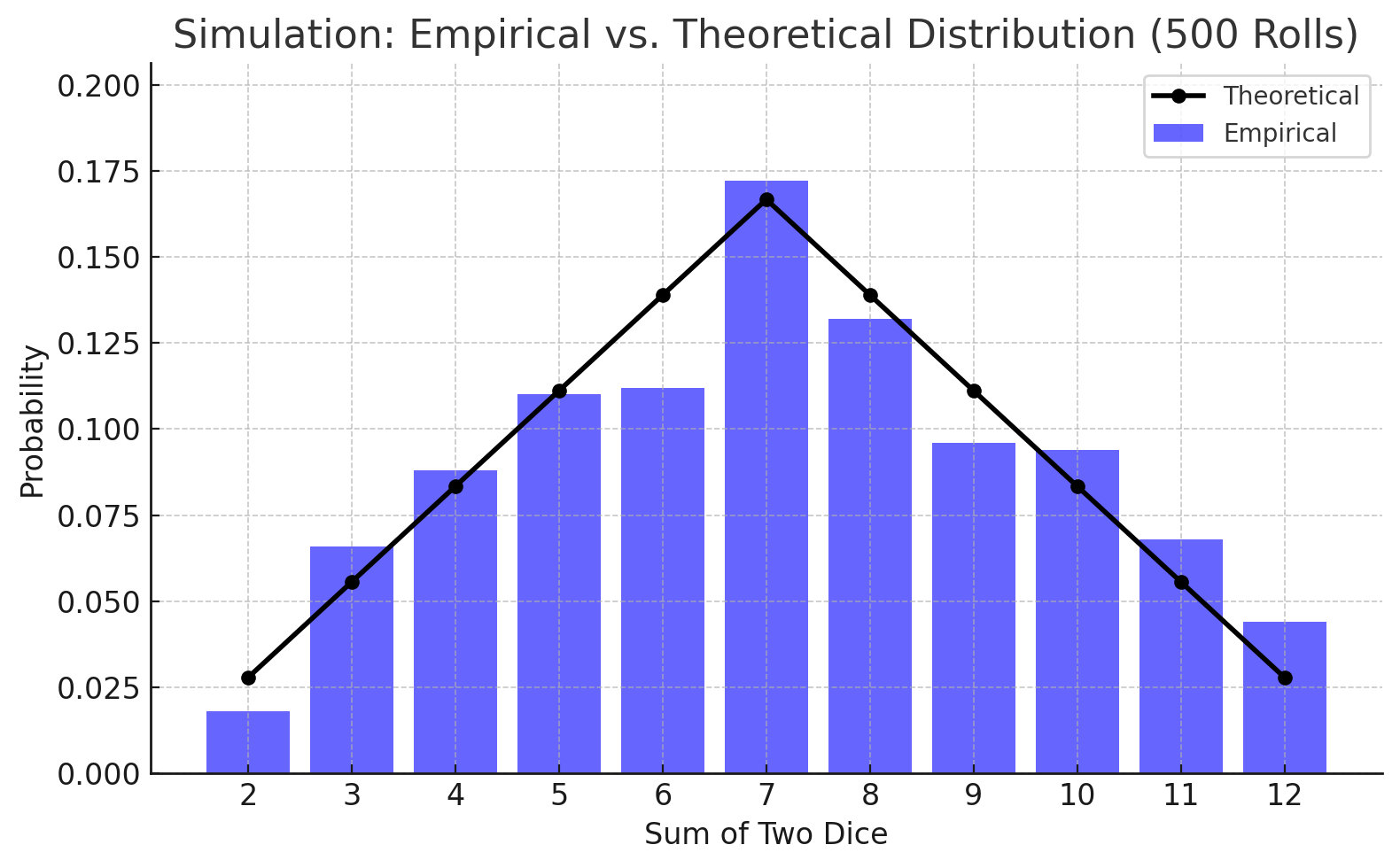
Distributions for 500 rolls

Distributions for 1,000 rolls

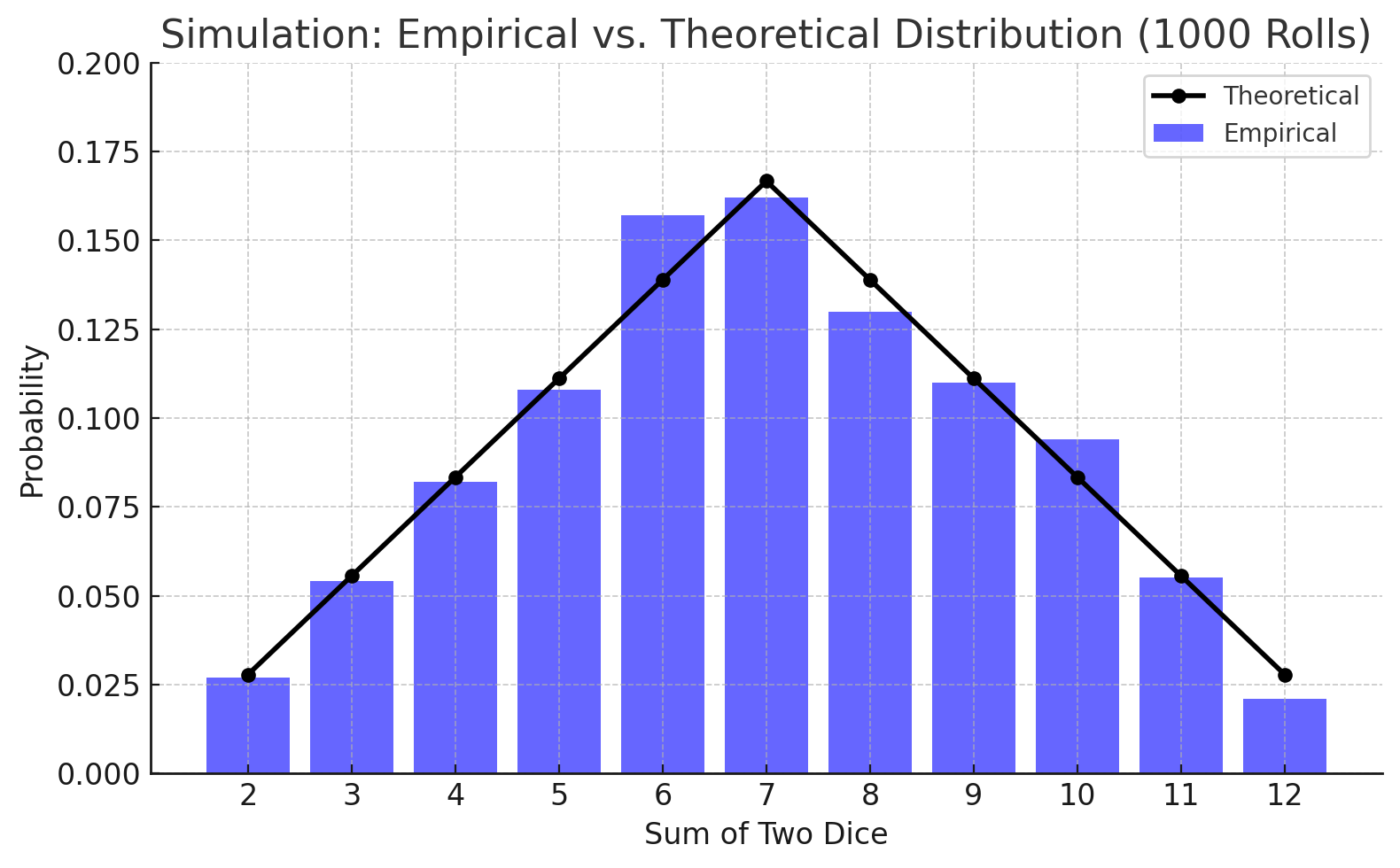
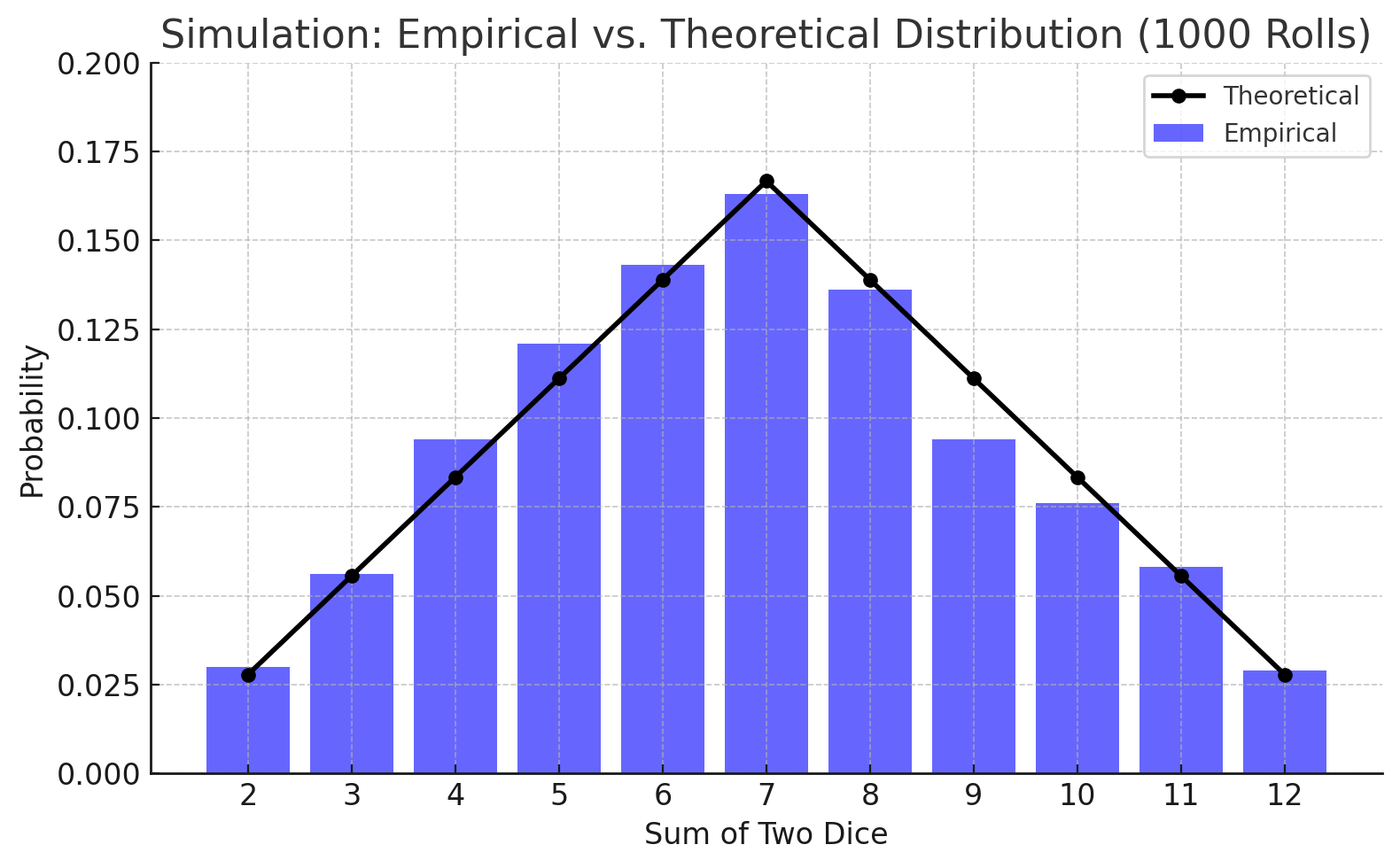
As we eventually reach 500 and then 1,000 roll simulations, we can clearly see that the empirical distributions start to approach their theoretical values. This generally matches our expectations with probability theory and hopefully will not be too surprising. Most Catan games, however do not last 1,000 turns, which is unfortunate for dice distributions but fortunate for our limited time.

End game - Impact on strategy

Armed with this information on dice rolls and probability, how should we set ourselves up to succeed in future Catan games?

This answer may be unsatisfying, but unfortunately there’s not much we can do differently going forward. In the absence of playing 500 turn games, it is still optimal to pick starting positions that are set up on higher probability hexes. Although the actual dice distribution will likely differ from theory, you should still seize every opportunity to give yourself the probabilistic edge. Selecting the higher probability hexes, in combination with some of the strategic elements mentioned by ChatGPT above, should put you in a great starting position.

If this is still bothering you and you truly can’t live with this level of randomness in your life, then there is one other solution. An online version of Catan, Colonist.io, actually provides a setting called “balanced dice” that is designed to mimic the theoretical distribution. So, if you can round up three friends who prefer to play online and escape some of the whims of fate, then this may be the best option. However, this means you can no longer complain about 4s rolling more often than 8s.